Большинство химических и биохи­мических процессов с ростом темпе­ратуры заметно ускоряются. Так, мясо при комнатной температуре испор­тится гораздо скорее, чем в холодиль­нике. В странах с влажным тропиче­ским климатом фрукты созревают раньше, а машины ржавеют быстрее,

чем в северных широтах. Железо не реагирует с холодной концентри­рованной серной кислотой, но раст­воряется в горячей.

Этот эффект ещё в XIX в. был описан с помощью эмпирического (т. е. выведенного из опытных дан­ных) правила Вант-Гоффа:

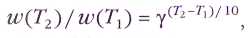
Даже по самому простому уравнению реакции нельзя сказать, является ли она элементарной или нет. Реакцию иода с водородом Н₂+I₂=2HI долгое время считали элементарной, потому что её скорость описывалась уравне­нием w = k[H₂][I₂], характерным для бимолекулярных реакций. Но потом выяснилось, что реакция эта сложная и состоит по меньшей мере из трёх элементарных. На первой стадии молекула иода при нагревании распа­дается на атомы: 1₂®^k12I. Атомы могут либо опять превратиться в молекулу иода: 2I®^k2I2, либо столк­нуться с молекулой водорода и обра­зовать две молекулы иодоводорода: 2I+Н₂®^k3HI

Зависимость концентрации реагента с от времени t для реакции первого по­рядка А®Р описывается формулой с=с₀е^-kt (с₀ — начальная концентра­ция исходного вещества А, к — кон­станта скорости реакции). Такая фор­мула называется экспоненциальной, а соответствующая кривая — экспонентой (спадающей). Для реакции второ­го порядка А+®Р(в простейшем случае равенства концентраций реа­гентов А и В) скорость описывается уравнением w=dc/dt=-кс² (знак «ми­нус» показывает, что концентрация уменьшается со временем). Интегри­рование этого уравнения дает иную за­висимость концентрации реагента А (или В) от времени: 1/с-1/с₀=kt, а со­ответствующая кинетическая кривая имеет гиперболическую зависимость (см. рисунок). Для реакций первого по­рядка период полупревращения t_1/2 — величина  постоянная:  t_1/2 =ln2/к.

Если реакции протекают при столкнове­нии молекул, то скорость реакций долж­на напрямую зависеть от числа этих столкновений, которое можно рассчи­тать на основе молекулярно-кинетической теории. Число встреч двух частиц х и у в единицу времени прямо пропор­ционально произведению их концентра­ций: z=const [x] [у], где постоянная (const) зависит от температуры, массы и размера сталкивающихся частиц.

Встречи двух частиц длятся не более 10^-12 с, частота же двойных соударений

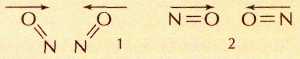
Столкновение двух молекул NO: 1 — хорошая ориентация для образования молекулы димера O=N—N=O(молекулы расположены «лицом» друг к другу); 2 — плохая ориентация («спиной» друг к другу).

Для того чтобы количественно опи­сать зависимость скорости от кон­центрации, надо понять, как «устро­ены» химические реакции.

Они редко бывают простыми. Как правило, реакция состоит из сложной последовательности отдельных стадий. Например, окисление фосфина подкисленным раствором перманганата калия описывается ионным уравнением 5РН₃+8МnО^-₄+19Н⁺=5Н₂РО^-₄+8Мn²⁺+12Н₂О. В левой части уравнения — 32 частицы. Ясно, что все они не способны встретить­ся одновременно. Они реагируют друг с другом поочерёдно, объединя­ясь в промежуточные частицы, кото­рые в свою очередь взаимодействуют с исходными веществами, образуя продукты реакции или другие проме­жуточные частицы.

Но процесс разделения сложной реакции на более простые не может продолжаться бесконечно. Есть такие реакции, которые уже не «упрощаются». Их называют элементарными.

Одна из основных задач химической кинетики -- управление скоростью реакции. Полезные реакции нужно заставить идти быстрее, а вредные — замедлить. Для этого надо знать, какие факторы влияют на их скорость.

Все химические превращения в растворе или в газовой фазе (за ис­ключением инициируемых светом) происходят при столкновении моле­кул. Чем чаще молекулы встречаются, тем быстрее идёт взаимодействие. Число же столкновений, а следова­тельно и скорость реакции, зависит от числа молекул в единице объёма, т. е. от концентраций реагирующих веществ.

Если бы при каждом столкновении молекулы вступали во взаимодейст­вие, все химические реакции закан­чивались бы мгновенно, многие — со взрывом. На самом деле некоторые молекулы при столкновении превра­щаются в продукты реакции, а дру­гие — нет. От чего это зависит?

Дело в том, что для разрыва или ослабления старых химических свя­зей нужна энергия. Когда сталкивают­ся активные молекулы, которые обла­дают некоторым запасом энергии, они могут прореагировать. Если же энергия мала, то столкновение не приводит к реакции и молекулы разлетаются без химического превра­щения. Энергия молекул в свою оче­редь зависит от температуры. Это и есть второй важнейший фактор, опре­деляющий скорость реакции. Подав­ляющее большинство реакций уско­ряется с ростом температуры.

Золотые украшения сохраняют свою красоту и блеск веками. А вот бро­шенный на улице старый автомо­биль спустя несколько лет превраща­ется в груду ржавого металлолома; долька яблока уже через несколько часов покрывается бурой плёнкой; пе­тарда, брошенная в костёр, оглуши­тельно взрывается.

Любопытно, что с точки зрения химической термодинамики воз­можны все перечисленные процессы, даже окисление золота. Просто у них разные скорости. Одной реакции требуются для завершения микросе­кунды, другой — миллионы лет. По­чему так? Термодинамика ответить бессильна: в этой теории не учитыва­ется время. Скорости химических ре­акций изучает химическая кинетика. Более того, химическая кинетика да­ёт ключ к управлению реакцией.

Полученный критерий самопроиз­вольного протекания реакции можно преобразовать в более удобную фор­му, если воспользоваться ещё одной термодинамической функцией — энергией Гиббса, которая обозначает­ся буквой G и определяется как G=Н-TS. Названа она в честь одного из основателей химической термоди­намики, американского учёного Джозайи Уилларда Гиббса (1839—1903).

Преобразуем выражение DS_общ =DS_сист-DH_сист/T>0, умножив  его на -Т. Получим:

-TDS_общ=-TDS_сист+DH<0. С учётом новой функции G последнее выражение приобретает вид -TDS_общ=DG_сист<0.

Теперь критерий самопроизволь­ности реакции и её равновесия мож­но выразить через изменение энер­гии Гиббса системы;

DG<0 — самопроизвольная реак­ция;

DG=0 — реакция находится в со­стоянии равновесия;

DG>0 — несамопроизвольная ре­акция (самопроизвольна обратная реакция).

Итак, энтропия — мера хаотичности, беспорядка. А наиболее хаотичной формой существования вещества яв­ляется газ. Поэтому если химическая реакция протекает с увеличением числа молей газов в системе, то эн­тропия системы возрастает, и наобо­рот. Например, энтропия сильно уве­личивается в реакции СаСО₃=СаО+СО₂ и уменьшается в реакции 2Н₂+О₂=2Н₂О.

Энтропия — царица хаоса.

Критерий самопроизвольности про­цесса устанавливается вторым за­коном термодинамики. Он имеет несколько формулировок, равнознач­ность которых не всегда очевидна на первый взгляд. Интересна история от­крытия этого закона.

В 1824 г. французский физик Нико­ла Леонар Сади Карно (1796—1832) в своей единственной опубликованной работе «Размышления о движущей си­ле огня и о машинах, способных раз­вивать эту силу» описал идеальную тепловую машину, позволяющую по­лучать максимальную работу за счёт использования теплоты. Он сделал важный вывод: для получения работы недостаточно иметь только источник теплоты (нагреватель), но необходим ещё и её приёмник. Карно утверждал, что тепловые машины совершают ра­боту не за счёт расхода теплорода, а за счёт его перехода от горячего тела к холодному, подобно тому как падение воды с высоты приводит в движение турбину (о теплороде рассказано в статье «Тепло химических реакций»). Коэффициент же полезного дейст­вия тепловой машины зависит ис­ключительно от разности температур нагревателя и теплоприёмника.

Для описания степени беспорядка используется особая термодинамиче­ская функция, называемая энтро­пией и обозначаемая буквой S. Это понятие (от греч. «эн» — «в», «внутрь» и «тропе» — «поворот», «превраще­ние») ввёл немецкий физик Рудольф Клаузиус в 18б5 г. «Слово „энтро­пия", — писал он, — я намеренно по­добрал ближе к слову „энергия", так как обе соответствующие этим выра­жениям величины настолько близки по своему смыслу, что они, по моему мнению, требуют однородного обо­значения».

Почему же природа ведёт себя та­ким образом, что необратимость всех процессов связана именно с рассея­нием энергии?

Чтобы ответить на этот вопрос, не­обходимо переместиться в мир атомов и молекул. Даже в состоянии термо­динамического равновесия части­цы ни на мгновение не прекра­щают своего беспорядочного движения.  Их скорости  и положения в пространстве по­стоянно меняются. Другими словами, одному макроско­пическому состоянию соот­ветствует великое множество микроскопических состоя­ний — различных вариантов положений всех частиц в про­странстве и их скоростей. Число микросостояний назы­вается термодинамической ве­роятностью W и характеризует неупорядоченность, хаотичность системы.

Молекулярную природу энтро­пии раскрыл австрийский физик Людвиг Больцман (1844—1906). Связь энтропии с молекулярным хаосом он описал формулой S=klnW, где k — постоянная величина, называемая константой Больцмана, которая свя­зана с газовой постоянной соотноше­нием k=R/N_A (N_A — постоянная Аво­гадро) и равна 1,38•10^-23 Дж/К

Марселен Бертло и датский химик Ханс Петер Юрген Юлиус Томсен (1826—1909) предположили, что самопроизвольно могут протекать только экзотермические (сопровож­дающиеся выделением теплоты) реак­ции. Действительно, как показывает опыт, такие реакции обычно идут самопроизвольно. Однако критерий Бертло—Томсена оказался неверным, поскольку впоследствии стали из­вестны и самопроизвольные эндотер­мические (протекающие с поглоще­нием теплоты) реакции, которые чаще всего идут при высоких темпе­ратурах. Таким образом, в природе существует некий общий закон, опре­деляющий направление самопроиз­вольных процессов.

В чём же его суть?