Содержание понятия – совокупность существенных признаков предмета, которое мыслится в данном понятии.
Объём понятия – совокупность предметов, которое мыслится в понятии.
Между содержанием и объёмом действует закон обратного отношения. Чем больше объём, тем меньше содержание, чем больше содержание, тем меньше объём.
Класс или множество – определённая совокупность предметов, имеющая некоторые признаки.
Подкласс
Классы состоят из элементов. Элемент – предмет, входящий в данный класс.
Универсальный( класс, состоящий из всех элементов, исследуемой области---Субъекты РФ), единичный( класс , состоящий из одного единственного элемента---созвездие Большая медведица), пулевой(пустой)(класс не содержащий ни одного элемента –НЛО)
Объём понятия – совокупность предметов, которое мыслится в понятии.
Между содержанием и объёмом действует закон обратного отношения. Чем больше объём, тем меньше содержание, чем больше содержание, тем меньше объём.
Класс или множество – определённая совокупность предметов, имеющая некоторые признаки.
Подкласс
Классы состоят из элементов. Элемент – предмет, входящий в данный класс.
Универсальный( класс, состоящий из всех элементов, исследуемой области---Субъекты РФ), единичный( класс , состоящий из одного единственного элемента---созвездие Большая медведица), пулевой(пустой)(класс не содержащий ни одного элемента –НЛО)
1. Логика происходит от греч. logos, что одновременно означает речь, слово, высказывание, понятие. Основатель логики Аристотель чаще всего употреблял термин "логос" в смысле "определения" или "разумности вообще".
Следовательно, предмет логики составляют:
* Законы, которым подчиняется мышление в процессе познания объективного мира.
* Формы мыслительного процесса - понятия, суждения и умозаключения.
* Методы получения нового выводного знания - сходства, различия сопутствующих изменений, остатков и другие.
* Способы доказательства истинности полученных знаний: прямое и косвенное доказательство, опровержение и т.д.
В современном понимании, логика - это наука о законах и формах правильного мышления.
2. Познание – это деятельность человека, направленная на приобретение знаний.
3. Ощущение — это отражение отдельных чувственно воспринимаемых свойств предметов — их цвета, формы, запаха, вкуса.
4. восприятие - целостный образ предмета, возникающий в результате его непосредственного воздействия на органы чувств.
5. Представление — это сохранившийся в сознании чувственный образ предмета, который воспринимался раньше.
6. Логическая форма - это строение конкретной мысли, способ связи ее составных частей. Л.ф. мысли можно выразить при помощи символов. S - субъект (понятие о предмете суждения), P - предикат (понятие о признаке предмета).
Следовательно, предмет логики составляют:
* Законы, которым подчиняется мышление в процессе познания объективного мира.
* Формы мыслительного процесса - понятия, суждения и умозаключения.
* Методы получения нового выводного знания - сходства, различия сопутствующих изменений, остатков и другие.
* Способы доказательства истинности полученных знаний: прямое и косвенное доказательство, опровержение и т.д.
В современном понимании, логика - это наука о законах и формах правильного мышления.
2. Познание – это деятельность человека, направленная на приобретение знаний.
3. Ощущение — это отражение отдельных чувственно воспринимаемых свойств предметов — их цвета, формы, запаха, вкуса.
4. восприятие - целостный образ предмета, возникающий в результате его непосредственного воздействия на органы чувств.
5. Представление — это сохранившийся в сознании чувственный образ предмета, который воспринимался раньше.
6. Логическая форма - это строение конкретной мысли, способ связи ее составных частей. Л.ф. мысли можно выразить при помощи символов. S - субъект (понятие о предмете суждения), P - предикат (понятие о признаке предмета).
Условные / импликация и эквиваленция / высказывания и условия их истинности. Условные (импликативные) суждения – состоящие из двух простых, соединённых логическим союзом если…то… Импликация (а > b) истинна во всех случаях, кроме одного: когда а - истнно, b - ложно.
Эквивалентное суждение – состоящее из двух простых, связанных двойной (прямой и обратной) зависимостью, выраженной логическим союзом если и только если, то…Эквиваленция (а b) истинна тогда, когда оба суждения истинны или оба ложны.
Достоверные и правдоподобные умозаключения.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений выводится новое суждение.
Достоверные умозаключения – когда заключение однозначно вытекает из посылок, однозначно истинное, представляет собой логический закон.
Правдоподобные - когда заключение с большей или меньшей вероятностью, но не обязательно вытекает из посылок.
Эквивалентное суждение – состоящее из двух простых, связанных двойной (прямой и обратной) зависимостью, выраженной логическим союзом если и только если, то…Эквиваленция (а b) истинна тогда, когда оба суждения истинны или оба ложны.
Достоверные и правдоподобные умозаключения.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений выводится новое суждение.
Достоверные умозаключения – когда заключение однозначно вытекает из посылок, однозначно истинное, представляет собой логический закон.
Правдоподобные - когда заключение с большей или меньшей вероятностью, но не обязательно вытекает из посылок.
Предмет логики.
Познание мира идёт двумя путями: с помощью чувств и с помощью разума (мышления).
Логика – наука о мышлении как средстве познания мира. Её предмет – законы, формы, приёмы и операции мышления. = Искусство мыслить.
Значение логики в познании и деятельности.
Учит сознательно применять законы, формы, приёмы и операции мышления, чтобы точно и последовательно мыслить, не допускать противоречий в рассуждениях. Повышает культуру мышления:
- Помогает выделить из массы сведений главное,
- развивает критическое отношение к своим и чужим мыслям,
- учит проверять правильность заключений и обосновывать выводы.
Определение понятий. Явные и неявные определения
Понятие – это форма мышления, отражающая предметы в их существенных признаках. Признак – то, в чём предметы сходны или отличны.
Определение – логическая операция, раскрывающая содержание понятия. Бывают номинальнами и реальными, явными и неявными.
Познание мира идёт двумя путями: с помощью чувств и с помощью разума (мышления).
Логика – наука о мышлении как средстве познания мира. Её предмет – законы, формы, приёмы и операции мышления. = Искусство мыслить.
Значение логики в познании и деятельности.
Учит сознательно применять законы, формы, приёмы и операции мышления, чтобы точно и последовательно мыслить, не допускать противоречий в рассуждениях. Повышает культуру мышления:
- Помогает выделить из массы сведений главное,
- развивает критическое отношение к своим и чужим мыслям,
- учит проверять правильность заключений и обосновывать выводы.
Определение понятий. Явные и неявные определения
Понятие – это форма мышления, отражающая предметы в их существенных признаках. Признак – то, в чём предметы сходны или отличны.
Определение – логическая операция, раскрывающая содержание понятия. Бывают номинальнами и реальными, явными и неявными.
1) противоречия – отношения между разными по качеству и по количеству суждениями: если одно истинно, то другое – нет.
2) противоположности – между общими, но разными по качеству суждениями: если одно истинно, другое ложно. Если оба ложны – одно может быть истинным.
3) подпротивоположности – между разными по качеству частными суждениями: не могут быть оба ложными, хотя бы одно истинно.
4) подчинения – между суждениями одинакового качества, но разного количества: если большее истинно, меньше тоже. Если большее ложно – меньшее м.б. и истинным, и ложным.
Логический квадрат: углы соответствуют суждениям, а стороны и диагонали - отношениям:
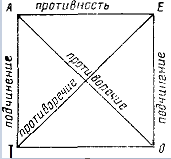
А-Е- противоположность; I-О – частичная совместимость.
2) противоположности – между общими, но разными по качеству суждениями: если одно истинно, другое ложно. Если оба ложны – одно может быть истинным.
3) подпротивоположности – между разными по качеству частными суждениями: не могут быть оба ложными, хотя бы одно истинно.
4) подчинения – между суждениями одинакового качества, но разного количества: если большее истинно, меньше тоже. Если большее ложно – меньшее м.б. и истинным, и ложным.
Логический квадрат: углы соответствуют суждениям, а стороны и диагонали - отношениям:

А-Е- противоположность; I-О – частичная совместимость.
Простое высказывание (суждение) – повествовательное предложение, включающее только одно суждение.
По качеству: утвердительные и отрицательные.
По количеству: единичные (об 1 предмете), частные (о некоторых предметах класса – некоторые, большинство, часть) и общие (обо всех предметах класса – никто, все).
Виды: общеутвердительные, общеотрицательные, частноутвердительные, частноотрицательные + выделяющие (только, некоторые, все) и исключающие (кроме, за исключением, помимо, не считая).
По качеству: утвердительные и отрицательные.
По количеству: единичные (об 1 предмете), частные (о некоторых предметах класса – некоторые, большинство, часть) и общие (обо всех предметах класса – никто, все).
Виды: общеутвердительные, общеотрицательные, частноутвердительные, частноотрицательные + выделяющие (только, некоторые, все) и исключающие (кроме, за исключением, помимо, не считая).
Умозаключения по логическому квадрату: можно строить отношения между категорическими суждениями, устанавливая истинность или ложность одного утверждения из истинности или ложности другого.
Отношения противоречия: А-О, Е-I. По закону исключения 3-его, если 1-е суждение истинно, то 2-е ложно. Если 1-е ложно – 2-е истинно.
Отношения противоположности: А-Е. Если 1-е суждение истинно, то 2-е ложно. Но если 1 ложно, 2-е не обязательно истинно (смотреть по смыслу).
Отношения частичной совместимости: I-О. Если 1-е ложно, 2-е истинно. Но если 1-е истинно, 2-е м.б. и ложно, и истинно. Оба ложными быть не могут.
Отношения подчинения: А-I, Е-О. если истинно 1-е (подчиняющее), истинно и 2-е (подчинённое), но не наоборот. Если 1-е ложно, 2-е ложно тоже, но не наоборот.
Отношения противоречия: А-О, Е-I. По закону исключения 3-его, если 1-е суждение истинно, то 2-е ложно. Если 1-е ложно – 2-е истинно.
Отношения противоположности: А-Е. Если 1-е суждение истинно, то 2-е ложно. Но если 1 ложно, 2-е не обязательно истинно (смотреть по смыслу).
Отношения частичной совместимости: I-О. Если 1-е ложно, 2-е истинно. Но если 1-е истинно, 2-е м.б. и ложно, и истинно. Оба ложными быть не могут.
Отношения подчинения: А-I, Е-О. если истинно 1-е (подчиняющее), истинно и 2-е (подчинённое), но не наоборот. Если 1-е ложно, 2-е ложно тоже, но не наоборот.
Дизъюнктивные высказывания – когда несколько простых суждения образуют сложное с помощью разделительного логического союза «\/» (дизъюнкция). Леса на территории нашей страны являются либо лиственными, либо хвойными, либо смешанными. Разделительные союзы – или, либо.
1) Слабая (нестрогая) дизъюнкция– не исключает одновременную истинность простых суждений, входящих в сложное. Леса бывают лиственными или хвойными, или смешанными. Сложное суждение ложно, только когда все его простые составляющие ложны. Истин¬но тогда, когда хотя бы одно его простое суждение истинно.
2) Строгая дизъюнкция – та, в которой члены дизъюнкции исключают друг друга. Данное животное есть или волк, или медведь. Сложное суждение истинно, когда только одно его простое суждение истинно.
В С В \/ С
и и и
л и и
и л и
л л л
Формула:
В v С v Д
1) Слабая (нестрогая) дизъюнкция– не исключает одновременную истинность простых суждений, входящих в сложное. Леса бывают лиственными или хвойными, или смешанными. Сложное суждение ложно, только когда все его простые составляющие ложны. Истин¬но тогда, когда хотя бы одно его простое суждение истинно.
2) Строгая дизъюнкция – та, в которой члены дизъюнкции исключают друг друга. Данное животное есть или волк, или медведь. Сложное суждение истинно, когда только одно его простое суждение истинно.
В С В \/ С
и и и
л и и
и л и
л л л
Формула:
В v С v Д
Оба эти фактора – условия достижения верных результатов в процессе рассуждения.
Истинность – соответствие действительности. Мысль, не соответствующая действительности – ложная.
Логическая правильность – умение правильно подобрать основы суждения и построить рассуждение по законам мышления, чтобы сделать истинные выводы. При нарушении законов логики даже из истинных суждений можно сделать неверные выводы.
Законы:
1) тождества,
2) не противоречия,
3) исключённого третьего и
4) достаточного основания.
Истинность – соответствие действительности. Мысль, не соответствующая действительности – ложная.
Логическая правильность – умение правильно подобрать основы суждения и построить рассуждение по законам мышления, чтобы сделать истинные выводы. При нарушении законов логики даже из истинных суждений можно сделать неверные выводы.
Законы:
1) тождества,
2) не противоречия,
3) исключённого третьего и
4) достаточного основания.
Научная индукция – умозаключение, в котором обобщение строится путём отбора необходимых и исключения случайных обстоятельств. На основании сопоставления сходства и различия и последующего исключения лишнего (остатков) делается обобщение.
Популярная индукция – обобщение, в котором путём перечисления устанавливается принадлежность признака некоторым предметам и на этой основе проблематично (под вопросом) заключают о его принадлежности всему классу.
Называется также индукцией через простое перечисление (статистику). Наблюдения за влиянием погоды на урожай и пр.
Популярная индукция – обобщение, в котором путём перечисления устанавливается принадлежность признака некоторым предметам и на этой основе проблематично (под вопросом) заключают о его принадлежности всему классу.
Называется также индукцией через простое перечисление (статистику). Наблюдения за влиянием погоды на урожай и пр.
Логический парадокс – ситуация, когда в теории доказываются два взаимно исключающие друг друга суждения, причем каждое из них выведено убедительными средствами. = Противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям. Высказывание, состоящее из двух суждений, которые взаимно отрицают друг друга, но которые равнодоказуемы и равновероятны.
- В деревне только один парикмахер, но он бреет только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?
- Если он себя не бреет, то он относится к тем жителям деревни, которых он должен брить. Значит, он должен себя брить. Если же он себя бреет, то он не относится к тем жителям своей деревни, которых он должен брить. Значит, он не должен себя брить.
Софизм (= логическая уловка) – преднамеренные нарушения логических правил с целью ввести в заблуждение слушателей или оппонента (противника в споре) или создать видимость победы в дискуссии. Софизмами намеренно запутывают, уводят от истины.
Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя есть рога.
- В деревне только один парикмахер, но он бреет только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?
- Если он себя не бреет, то он относится к тем жителям деревни, которых он должен брить. Значит, он должен себя брить. Если же он себя бреет, то он не относится к тем жителям своей деревни, которых он должен брить. Значит, он не должен себя брить.
Софизм (= логическая уловка) – преднамеренные нарушения логических правил с целью ввести в заблуждение слушателей или оппонента (противника в споре) или создать видимость победы в дискуссии. Софизмами намеренно запутывают, уводят от истины.
Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя есть рога.
Определение должно быть истинно по содержанию и правильно по строению и форме.
1. Должно быть соразмерным (объём определяющего = объёму определяемого): Кинология – это наука – слишком широко; кинология – это наука о служебных собаках – слишком узко; кинология – это наука о собаках – правильно.
2. Не должно содержать в себе круга (объяснять непонятное через то же самое или через что-то, что определяется первым понятием). Идеалист – это человек идеалистических убеждений.
3. Должно быть ясным, указывать на известные признаки, не нуждающиеся в определении и не содержащие двусмысленности: индетерминизм – это противоположность детерминизму – неверно: понятие детеминизма само нуждается в определении.
4. Не должно быть отрицательным (указывать, чем не является предмет): поезд – это не помидор.
1. Должно быть соразмерным (объём определяющего = объёму определяемого): Кинология – это наука – слишком широко; кинология – это наука о служебных собаках – слишком узко; кинология – это наука о собаках – правильно.
2. Не должно содержать в себе круга (объяснять непонятное через то же самое или через что-то, что определяется первым понятием). Идеалист – это человек идеалистических убеждений.
3. Должно быть ясным, указывать на известные признаки, не нуждающиеся в определении и не содержащие двусмысленности: индетерминизм – это противоположность детерминизму – неверно: понятие детеминизма само нуждается в определении.
4. Не должно быть отрицательным (указывать, чем не является предмет): поезд – это не помидор.