Построение деревьев классификации выполняется в следующей последовательности.
1. Определяется критерий качества дерева.
- Довольно часто минимизируется процент неправильно определенных элементов.
- Если размеры классификационных групп сильно различаются, то для снижения общей ошибки классификации лучше уделить больше внимания большей группе, постаравшись снизить вероятность ошибки для нее. Чтобы учесть размеры групп, программы построения деревьев классияикации допускают ввод априорных вероятностей попасть в ту или иную группу. Их можно
- взять равными;
- определить по имеющемуся набору случаев;
- взять из данных прошлых исследований.
- Минимизируется не вероятность ошибок, а их стоимость. Например, при сегментировании рынка продажи товаров по почте возможная реакция адресатов на почтовое предложение корреспондент может
- не ответить; при этом фирма потерпит небольшие убытки на отправку письма;
- потребовать прислать каталог, но ничего потом не купить. В этой ситуации убытки составляют не только стоимость пересылки, но и стоимость каталога;
- заказать товары, что принесет заметную прибыль.
В этой ситуации различные ошибки классификации имеют различную денежную оценку. Лучше разослать несколько писем впустую, чем пропустить одного покупателя. Поэтому многие программы допускают ввод оценки для каждого ожидаемого результата.
2. Выбирается алгоритм построения дерева. Различные конфигурации групп наилучшим образом отображаются различными алгоритмами. Можно либо оценить применимость того или иного метода по визуализированным исходным данным, либо испробовать различные методы, задавая различные режимы работы программы. Вот некоторые рекомнедации:
- если видно, что каждое разделение на группы происходит по значению одного признака, аналогично, то это говорит в пользу алгоритма CART;
- если линии, разделяющие группы, не параллельны осям, что начать следует с алгоритма QUEST;
- если же имеются переменные, измеренные в номинальных шкалах, причем число различных значений велико, то результат, скорее всего, будет проще при использовании алгоритма CHAID. Примером здесь служат такие вопросы, как профессия, любимые марки того или иного товара, читаемые газеты или любимые телеканалы.
3. Определяется правило окончания ветвлений, которое влияет на размер дерева.
В измерениях может присутствовать случайный шум, или области для различных групп могут пересекаться, поэтому дерево, точно классифицирующее имеющиеся случаи, окажется неадекватным и будет давать большие ошибки при классификации новых случаев. Эта ситуация показана на рисРис. 34). Ее отличие от рисРис. 32 заключается в том, что появился случайный шум, от чего границы разделения областей несколько размылись. Именно такой вид имеют данные исследований в подавляющем большинстве случаев. Пусть классификация имеющихся случаев произведена без ошибок. На основе правила, задаваемого полученным деревом, можно построить ломаные линии, разделяющие области (показаны на рисунке). Но дерево в этом случае получается слишком сложным, ведь каждый отрезок должен отдельно оговариваться в полученном правиле! Более того, при классификации новых случаев ошибка будет довольно большой. Ошибка классификации новых случаев была бы меньше, если бы линии разделения областей по-прежнему представляли бы собой прямые
Зависимость ошибки классификации от размера дерева (числа его узлов) показана на рисРис. 35. Видно, что для ошибки классификации новых случаев (а именно для этого и строится дерево) имеется минимум. Он достигается тогда, когда правило, отраженное в дереве классификации, учитывает лишь закономерности ситуации, пренебрегая случайным шумом.

Поэтому размер дерева следует ограничить. Можно задать:
- минимально допустимое количество элементов в узле;
- минимальный процент элементов в узле от общего числа элементов исследования;
- максимальное число узлов дерева;
- максимальную «глубину» ветвлений (например, задается, что от вершины до каждого узла не должно быть более трех ветвлений);
Некоторые программы используют ряд дополнительных алгоритмов, позволяющих получить более точное решение.
- Автоматический поиск минимума ошибки для новых случаев. Для этого все имеющиеся случаи разбиваются на две (обычно неравные) части случайным образом. Одна часть (обычно большая) используется для обучения, а другая – для проверки.
- Построение нескольких деревьев, максимально отличающихся друг от друга, с последующим выбором наилучшего.
- Использование нечеткого порога. Каждая ветвь получаемого дерева оценивается качеством прогноза. При этом оценка может быть низкой («плохой»), высокой («хорошеей») или промежуточной («сомнительной»). При классификации отбрасываются только те ветви, для которых оценка качества прогноза ниже заданного порога для «плохих» решений. «Сомнительные» ветви остаются для дальнейшего анализа вместе с «хорошими».
- Ручное «выращивание» каждой ветви шаг за шагом.
4. Вид представления полученных правил. Их можно представить в различной форме:
- для работы маркетологов удобно получить словесное описание сегментов;
- для формирования списка из базы данных можно создать запроса к базе данных на языке SQL.
***
Таким образом, деревья решений – мощное средство получения классифицирующих правил.
1. Определяется критерий качества дерева.
- Довольно часто минимизируется процент неправильно определенных элементов.
- Если размеры классификационных групп сильно различаются, то для снижения общей ошибки классификации лучше уделить больше внимания большей группе, постаравшись снизить вероятность ошибки для нее. Чтобы учесть размеры групп, программы построения деревьев классияикации допускают ввод априорных вероятностей попасть в ту или иную группу. Их можно
- взять равными;
- определить по имеющемуся набору случаев;
- взять из данных прошлых исследований.
- Минимизируется не вероятность ошибок, а их стоимость. Например, при сегментировании рынка продажи товаров по почте возможная реакция адресатов на почтовое предложение корреспондент может
- не ответить; при этом фирма потерпит небольшие убытки на отправку письма;
- потребовать прислать каталог, но ничего потом не купить. В этой ситуации убытки составляют не только стоимость пересылки, но и стоимость каталога;
- заказать товары, что принесет заметную прибыль.
В этой ситуации различные ошибки классификации имеют различную денежную оценку. Лучше разослать несколько писем впустую, чем пропустить одного покупателя. Поэтому многие программы допускают ввод оценки для каждого ожидаемого результата.
2. Выбирается алгоритм построения дерева. Различные конфигурации групп наилучшим образом отображаются различными алгоритмами. Можно либо оценить применимость того или иного метода по визуализированным исходным данным, либо испробовать различные методы, задавая различные режимы работы программы. Вот некоторые рекомнедации:
- если видно, что каждое разделение на группы происходит по значению одного признака, аналогично, то это говорит в пользу алгоритма CART;
- если линии, разделяющие группы, не параллельны осям, что начать следует с алгоритма QUEST;
- если же имеются переменные, измеренные в номинальных шкалах, причем число различных значений велико, то результат, скорее всего, будет проще при использовании алгоритма CHAID. Примером здесь служат такие вопросы, как профессия, любимые марки того или иного товара, читаемые газеты или любимые телеканалы.
3. Определяется правило окончания ветвлений, которое влияет на размер дерева.
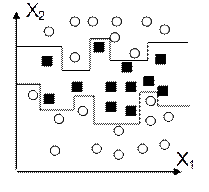
В измерениях может присутствовать случайный шум, или области для различных групп могут пересекаться, поэтому дерево, точно классифицирующее имеющиеся случаи, окажется неадекватным и будет давать большие ошибки при классификации новых случаев. Эта ситуация показана на рисРис. 34). Ее отличие от рисРис. 32 заключается в том, что появился случайный шум, от чего границы разделения областей несколько размылись. Именно такой вид имеют данные исследований в подавляющем большинстве случаев. Пусть классификация имеющихся случаев произведена без ошибок. На основе правила, задаваемого полученным деревом, можно построить ломаные линии, разделяющие области (показаны на рисунке). Но дерево в этом случае получается слишком сложным, ведь каждый отрезок должен отдельно оговариваться в полученном правиле! Более того, при классификации новых случаев ошибка будет довольно большой. Ошибка классификации новых случаев была бы меньше, если бы линии разделения областей по-прежнему представляли бы собой прямые

Рис. 34. Результат построения дерева классификации при наличии частичного перекрытия областей
Зависимость ошибки классификации от размера дерева (числа его узлов) показана на рисРис. 35. Видно, что для ошибки классификации новых случаев (а именно для этого и строится дерево) имеется минимум. Он достигается тогда, когда правило, отраженное в дереве классификации, учитывает лишь закономерности ситуации, пренебрегая случайным шумом.

Рис. 35. Зависимость ошибки классификации от размера дерева
Поэтому размер дерева следует ограничить. Можно задать:
- минимально допустимое количество элементов в узле;
- минимальный процент элементов в узле от общего числа элементов исследования;
- максимальное число узлов дерева;
- максимальную «глубину» ветвлений (например, задается, что от вершины до каждого узла не должно быть более трех ветвлений);
Некоторые программы используют ряд дополнительных алгоритмов, позволяющих получить более точное решение.
- Автоматический поиск минимума ошибки для новых случаев. Для этого все имеющиеся случаи разбиваются на две (обычно неравные) части случайным образом. Одна часть (обычно большая) используется для обучения, а другая – для проверки.
- Построение нескольких деревьев, максимально отличающихся друг от друга, с последующим выбором наилучшего.
- Использование нечеткого порога. Каждая ветвь получаемого дерева оценивается качеством прогноза. При этом оценка может быть низкой («плохой»), высокой («хорошеей») или промежуточной («сомнительной»). При классификации отбрасываются только те ветви, для которых оценка качества прогноза ниже заданного порога для «плохих» решений. «Сомнительные» ветви остаются для дальнейшего анализа вместе с «хорошими».
- Ручное «выращивание» каждой ветви шаг за шагом.
4. Вид представления полученных правил. Их можно представить в различной форме:
- для работы маркетологов удобно получить словесное описание сегментов;
- для формирования списка из базы данных можно создать запроса к базе данных на языке SQL.
***
Таким образом, деревья решений – мощное средство получения классифицирующих правил.
Источник: Н. В. Павлов, Санкт-Петербург, Издательство СПбГТУ, 2005
Авторское право на материал
Копирование материалов допускается только с указанием активной ссылки на статью!
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Похожие статьи