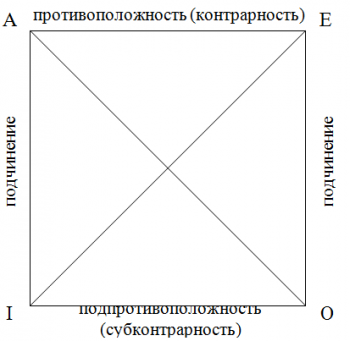
Для наглядности в логике используется понятие «логического квадрата», по углам которого располагаются суждения А, Е, I, O, а его стороны и диагонали являются символическим выражением основных логических отношений между суждениями.



I. Отношением подчинения связаны суждения A и I, E и O.
А Общие суждения (А, Е) являются подчиняющими, а частные (I, O) – подчинёнными. Для суждений, находящихся в
Е отношении подчинения, имеет значение следующее условие истинности: если истинно А, то истинно и I; если истинно Е, то также истинно и О, но не наоборот. Действительно, если истинно, что «Все студенты сдают зачет по
О логике» (А), то то же самое верно и относительно некоторых из них (I) «Некоторые студенты сдают зачет по логике», но не наоборот. Из того, что «Некоторые дни недели являются нерабочими» (I), вовсе не следует, что «Все дни недели являются нерабочими» (А).Если истинно суждение
«Ни один месяц не содержит тридцать второго числа» (Е), то истинным будет также подчиненное ему частно отрицательное суждение «В некоторых месяцах нет тридцать второго числа» (О).Обратное не верно. Из истинности частно отрицательного суждения «Некоторые плоды не являются съедобными» (0) не следует, что и «Ни один из плодов не употребляется в пищу» (Е).

II. В отношении противоречия находятся суждения Е и I, и А А и О. Согласно законам логики, два противоречивых суждения не могут быть одновременно ни истинными, ни ложными. Значит, в двузначной логике они будут принимать разные логические значения: I если А – истинно, то О – ложно О если А – ложно, то О – истинно
если О – истинно, то А – ложно если О – ложно, то А – истинно если E – истинно, то I – ложно если E – ложно, то I – истинно если I – истинно, то E – ложно если I – ложно, то E – истинно


или А ≡ ┐О, или ┐A ≡ O, или O ≡ ┐A, или ┐O ≡ A, или E ≡ ┐I, или ┐E ≡ I, или I ≡ ┐E, или ┐I ≡ E.


Установив вид одного из противоречивых суждений и его логическое значение, можно без труда установить также логическое значение противоречивого ему суждения. На- пример, зная, что суждение «Ни один дельфин не живет на суше» (Е) является истинным, заключают, что противоре- чивое ему суждение «Некоторые дельфины способны жить на суше» (I) - ложно.

А III Отношением контрарности связаны только общие суждения А и Е. Как мы уже знаем, контрарность означает противоположность, крайние позиции и не охватывает весь класс предметов. Здесь возможно «и третье», «и четвертое» … . Значит, контрарные суждения не обязательно
должны принимать разные логические значения. Верхняя О грань квадрата связывает такие виды суждений (А, Е), ко- торые могут быть одновременно ложными, но не могут
быть одновременно истинными. Например, оба суждения:
«Все люди любят музыку Шнитке» и «Ни один человек не любит музыку Шнитке» очевидно ложны. Истинное суж-
дение при этом будет выражать последний тип отношения
- субконтрарность.

IV Отношение субконтрарности может возникать только между частными суждениями I и O. Это отношение выражено нижней гранью квадрата. Помня о том, что суждения I и O Е подчинены суждениям А и Е, и беря во внимание отношение противоположности между суждениями А и Е, заключаем, что поскольку суждение А и О, Е и I связаны законом непротиворечия, то в случае контрарных отношений
О между А и Е отношения подчинения I→A и O→E «отменяются». В том случае, когда «верхние» суждения А и Е оказываются оба ложными (как в нашем примере), то истинными оказываются противоречащие им «нижние» суждения I и О. Поскольку суждения А и Е могут оказаться одновременно ложными, но не могут быть одновременно истинными, то суждения I и О, наоборот, могут быть одно- временно истинными, но не могут быть одновременно ложными (это и означает субконтрарность). Значит, в нашем примере истинными будут суждения: «Некоторые люди любят музыку Шнитке» (I), «Некоторые люди не лю- бят музыку Шнитке» (О).

Установление логических отношений между суждениями «по логическому квадрату позволяет производить ряд практических операций с суждениями. Например, зная истинное значение одного из суждений A, E, I, O, при помощи логического квадрата можно установить истинное значение трех остальных суждений.
Данная логическая операция в формальном виде предстает в виде решения «задачи по логическому квадрату». Например, необходимо установить, каково логическое значение суждений E, I, O, если А – суждение истинное.
Итак, А - истина
Е - ?
I - ?
O - ?
Решение задачи:
1. Выясняем значение другого общего суждения Е. Оно связано с А логическим отношением контрарности и также истинным быть не может (по определению контрарности). Значит, Е – ложно.

2. Устанавливаем значения суждений I и О, связанных с общими суждения- ми А и Е отношением противоречия. Поскольку при таком отношении суждения принимают разные логические значения, устанавливаем: если А истинно, то О – ложно; если Е ложно, то I – истинно.

Таким образом, решив задачу, устанавливаем, что:
Если А - истина, то
Е - ложь
I - истина
O - ложь